Topological Sort

Topological sorting of vertices of a Directed Acyclic Graph is an ordering of the vertices $v_1,v_2,...v_n$ in such a way, that if there is an edge directed towards vertex $v_j$ from vertex $v_i$, then $v_i$ comes before $v_j$. For example consider the graph given below:

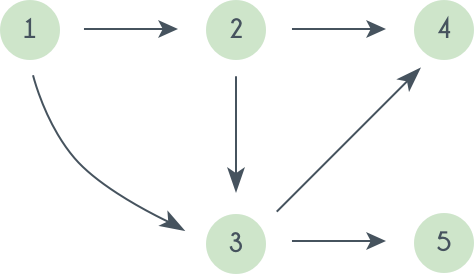
A topological sorting of this graph is: $1$ $2$ $3$ $4$ $5$
There are multiple topological sorting possible for a graph. For the graph given above one another topological sorting is: $1$ $2$ $3$ $5$ $4$
In order to have a topological sorting the graph must not contain any cycles. In order to prove it, let's assume there is a cycle made of the vertices $v_1,v_2,v_3...v_n$. That means there is a directed edge between $v_i$ and $v_{i+1}$ $(1\le i<n)$ and between $v_n$ and $v_1$. So now, if we do topological sorting then $v_n$ must come before $v_1$ because of the directed edge from $v_n$ to $v_1$. Clearly, $v_{i+1}$ will come after $v_i$, because of the directed from $v_i$ to $v_{i+1}$, that means $v_1$ must come before $v_n$. Well, clearly we've reached a contradiction, here. So topological sorting can be achieved for only directed and acyclic graphs.

Le'ts see how we can find a topological sorting in a graph. So basically we want to find a permutation of the vertices in which for every vertex $v_i$, all the vertices $v_j$ having edges coming out and directed towards $v_i$ comes before $v_i$. We'll maintain an array $T$ that will denote our topological sorting. So, let's say for a graph having $N$vertices, we have an array $in\mathrm{\_}degree[]$ of size $N$ whose $i^{th}$ element tells the number of vertices which are not already inserted in $T$ and there is an edge from them incident on vertex numbered $i$. We'll append vertices $v_i$ to the array $T$, and when we do that we'll decrease the value of $in\mathrm{\_}degree[v_j]$ by $1$ for every edge from $v_i$ to $v_j$. Doing this will mean that we have inserted one vertex having edge directed towards $v_j$. So at any point we can insert only those vertices for which the value of $in\mathrm{\_}degree[]$ is $0$.
The algorithm using a BFS traversal is given below:

topological_sort(N, adj[N][N])
        T = []
        visited = []
        in_degree = []
        for i = 0 to N
                in_degree[i] = visited[i] = 0

        for i = 0 to N
                for j = 0 to N
                        if adj[i][j] is TRUE
                                in_degree[j] = in_degree[j] + 1

        for i = 0 to N
                if in_degree[i] is 0
                        enqueue(Queue, i)
                        visited[i] = TRUE

        while Queue is not Empty
                vertex = get_front(Queue)
                dequeue(Queue)
                T.append(vertex)
                for j = 0 to N
                        if adj[vertex][j] is TRUE and visited[j] is FALSE
                                in_degree[j] = in_degree[j] - 1
                                if in_degree[j] is 0
                                        enqueue(Queue, j)
                                        visited[j] = TRUE
        return T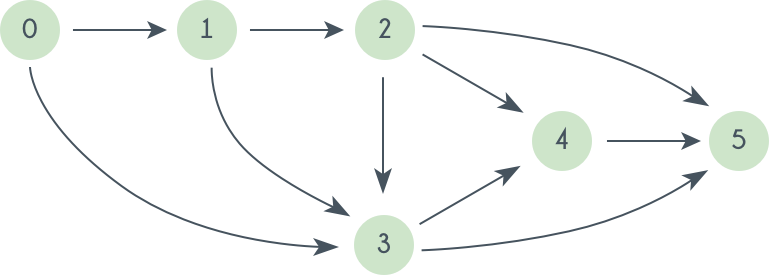

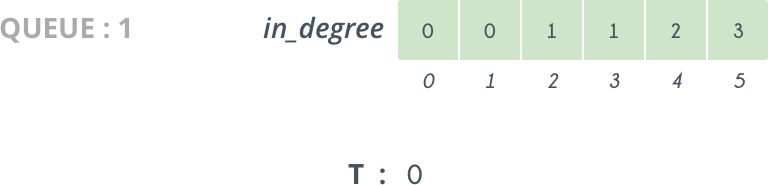
Let's take a graph and see the algorithm in action. Consider the graph given below:

Initially $in\mathrm{\_}degree[0]=0$ and $T$ is empty

So, we delete $0$ from $Queue$ and append it to $T$. The vertices directly connected to $0$ are $1$ and $2$ so we decrease their $in\mathrm{\_}degree[]$ by $1$. So, now $in\mathrm{\_}degree[1]=0$ and so $1$ is pushed in $Queue$.

Next we delete $1$ from $Queue$ and append it to $T$. Doing this we decrease $in\mathrm{\_}degree[2]$ by $1$, and now it becomes $0$ and $2$ is pushed into $Queue$.

So, we continue doing like this, and further iterations looks like as follows:

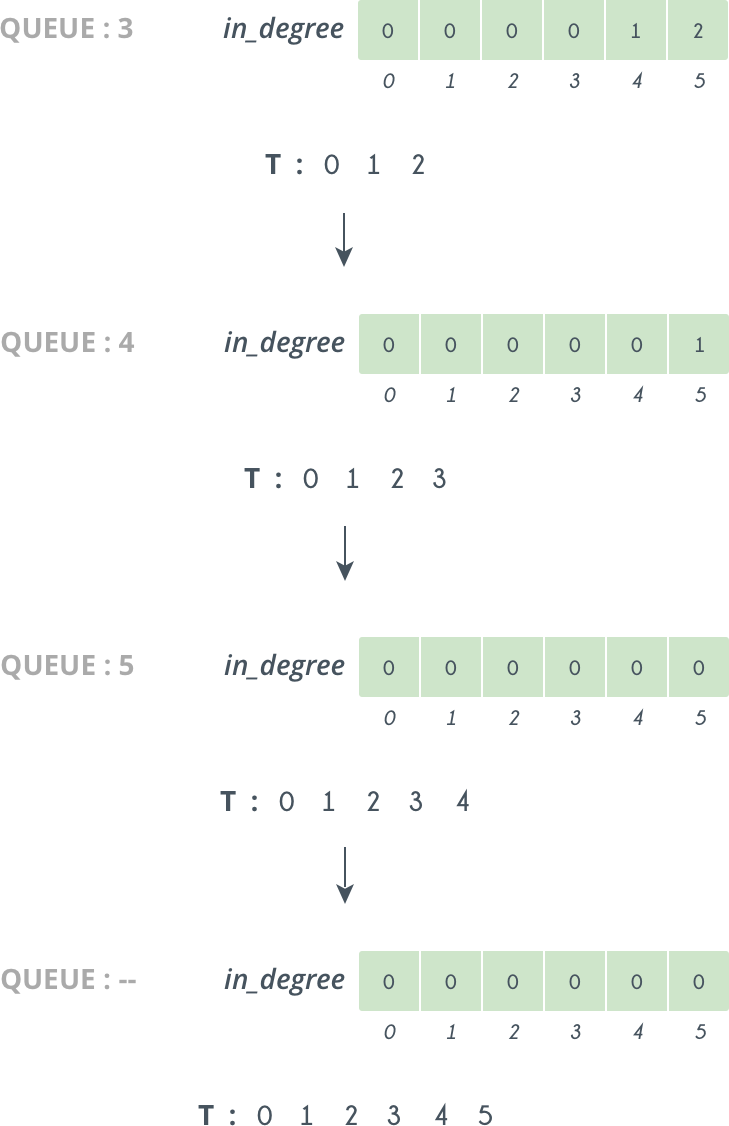
So at last we get our Topological sorting in $T$ i.e. : $0$, $1$, $2$, $3$, $4$, $5$

Solution using a DFS traversal, unlike the one using BFS, does not need any special $in\mathrm{\_}degree[]$ array. Following is the pseudo code of the DFS solution:

T = []
visited = []

topological_sort( cur_vert, N, adj[][] ){
    visited[cur_vert] = true
    for i = 0 to N
        if adj[cur_vert][i] is true and visited[i] is false
        topological_sort(i)
    T.insert_in_beginning(cur_vert)
}

The following image of shows the state of stack and of array $T$ in the above code for the same graph shown above.