Selection Sort

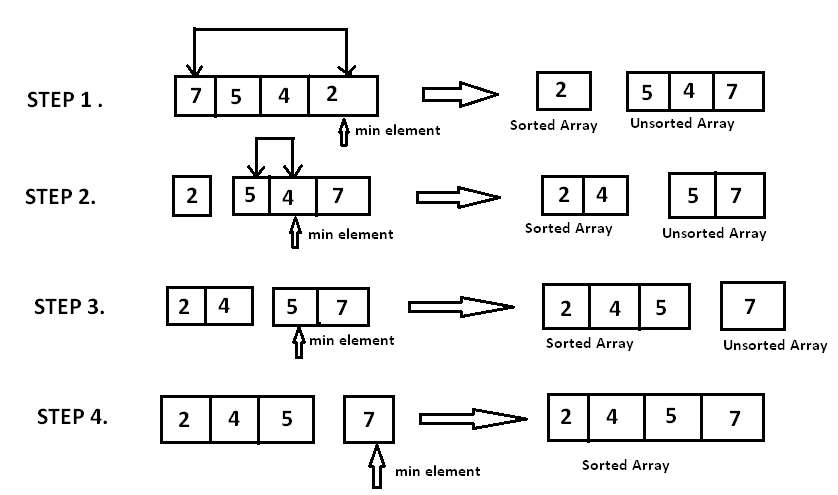
The Selection sort algorithm is based on the idea of finding the minimum or maximum element in an unsorted array and then putting it in its correct position in a sorted array.

Assume that the array $A=[7,5,4,2]$ needs to be sorted in ascending order.

The minimum element in the array i.e. $2$ is searched for and then swapped with the element that is currently located at the first position, i.e. $7$. Now the minimum element in the remaining unsorted array is searched for and put in the second position, and so on.

Let’s take a look at the implementation.

void selection_sort (int A[ ], int n) {
        // temporary variable to store the position of minimum element

        int minimum;        
        // reduces the effective size of the array by one in  each iteration.

        for(int i = 0; i < n-1 ; i++)  {

           // assuming the first element to be the minimum of the unsorted array .
             minimum = i ;

          // gives the effective size of the unsorted  array .

            for(int j = i+1; j < n ; j++ ) {
                if(A[ j ] < A[ minimum ])  {                //finds the minimum element
                minimum = j ;
                }
             }
          // putting minimum element on its proper position.
          swap ( A[ minimum ], A[ i ]) ; 
        }
   }

At $i^{th}$ iteration, elements from position $0$ to $i-1$ will be sorted.

Time Complexity:

To find the minimum element from the array of $N$ elements, $N-1$ comparisons are required. After putting the minimum element in its proper position, the size of an unsorted array reduces to $N-1$ and then $N-2$comparisons are required to find the minimum in the unsorted array.

Therefore $(N-1)$ + $(N-2)$ + $.......$ + $1$ = $(N\cdot (N-1))/2$ comparisons and $N$ swaps result in the overall complexity of $O(N^2)$.