Basic of stacks

Stacks are dynamic data structures that follow the Last In First Out (LIFO) principle. The last item to be inserted into a stack is the first one to be deleted from it.

For example, you have a stack of trays on a table. The tray at the top of the stack is the first item to be moved if you require a tray from that stack.

Inserting and deleting elements

Stacks have restrictions on the insertion and deletion of elements. Elements can be inserted or deleted only from one end of the stack i.e. from the $top$. The element at the top is called the $top$ element. The operations of inserting and deleting elements are called $push()$ and $pop()$ respectively.

When the top element of a stack is deleted, if the stack remains non-empty, then the element just below the previous top element becomes the new top element of the stack.

For example, in the stack of trays, if you take the tray on the top and do not replace it, then the second tray automatically becomes the top element (tray) of that stack.

Features of stacks

• Dynamic data structures
• Do not have a fixed size
• Do not consume a fixed amount of memory
• Size of stack changes with each $push()$ and $pop()$ operation. Each $push()$ and $pop()$ operation increases and decreases the size of the stack by $1$, respectively.

A stack can be visualized as follows:

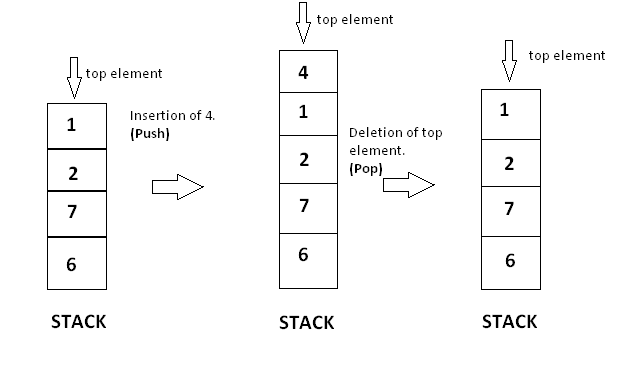
Operations

push( x ): Insert element x at the top of a stack

void push (int stack[ ] , int x , int n) {
 if ( top == n-1 ) {         //If the top position is the last of position in a stack, this means that the stack is full
    cout << “Stack is full.Overflow condition!” ;
    }
    else{
        top = top +1 ;            //Incrementing top position 
        stack[ top ] = x ;       //Inserting element on incremented position  
    }
}

pop( ): Removes an element from the top of a stack

   void pop (int stack[ ] ,int n ) 
    {

        if( isEmpty ( ) )
        {
            cout << “Stack is empty. Underflow condition! ” << endl ;
        }
        else    
        {
             top = top - 1 ; //Decrementing top’s position will detach last element from stack            
        }
    }

topElement ( ): Access the top element of a stack

  int topElement ( )
    {
        return stack[ top ];
    }

isEmpty ( ) : Check whether a stack is empty

    bool isEmpty ( )
    {
        if ( top == -1 )  //Stack is empty
        return true ; 
        else
        return false;
    }

size ( ): Determines the current size of a stack

   int size ( )
    {
        return top + 1;
    }

Implementation

#include <iostream>
using namespace std;
int top = -1; //Globally defining the value of top as the stack is empty

    void push (int stack[ ] , int x , int n)
    {
        if ( top == n-1 )       //If the top position is the last of position of the stack, this means that the stack is full.
        {
            cout << "Stack is full.Overflow condition!" ;
        }
        else
        {
            top = top +1 ;            //Incrementing the top position 
            stack[ top ] = x ;       //Inserting an element on incremented position  
        }
    }
    bool isEmpty ( )
    {
        if ( top == -1 )  //Stack is empty
            return true ; 
        else
            return false;
    }
    void pop ( ) 
    {

        if( isEmpty ( ) )
        {
            cout << "Stack is empty. Underflow condition! " << endl ;
        }
        else    
        {
             top = top - 1 ; //Decrementing top’s position will detach last element from stack            
        }
    }
    int size ( )
    {
        return top + 1;
    }
    int topElement (int stack[])
    {
        return stack[ top ];
    }
    //Let's implement these functions on the stack given above 

    int main( )
    {
        int stack[ 3 ];
        // pushing element 5 in the stack .
        push(stack , 5 , 3 ) ;

        cout << "Current size of stack is " << size ( ) << endl ;

        push(stack , 10 , 3);
        push (stack , 24 , 3) ;

        cout << "Current size of stack is " << size( ) << endl ;

        //As the stack is full, further pushing will show an overflow condition.
        push(stack , 12 , 3) ;

        //Accessing the top element
        cout << "The current top element in stack is " << topElement(stack) << endl;

        //Removing all the elements from the stack
        for(int i = 0 ; i < 3;i++ )
            pop( );
        cout << "Current size of stack is " << size( ) << endl ;

        //As the stack is empty , further popping will show an underflow condition.
        pop ( );  

    }

Output

• Current size of stack: 1
• Current size of stack: 3
• Current top element in stack: 24 (Stack is full. Overflow condition!)
• Current size of stack: 0 (Stack is empty. Underflow condition!)

Refer to the following image for more information about the operations performed in the code.

Application

Consider the balanced parentheses problem.

You have a bracket sequence made up of opening '(' and closing ')' parentheses. You must check if this bracket sequence is balanced.

A bracket sequence is considered balanced if for every prefix of the sequence, the number of opening brackets is greater than or equal to the number of closing brackets, and the total number of opening brackets is equal to the number of closing brackets.

You can check this using stack. Let's see how.

You can maintain a stack where you store a parenthesis. Whenever, you come across an opening parenthesis, $push$ it in the stack. However, whenever you come across a closing parenthesis, $pop$ a parenthesis from the stack.

    #include <iostream>
    using namespace std;
    int top;
    void  check (char str[ ], int n, char stack [ ])
    {
        for(int i = 0 ; i < n ; i++ )
        {
            if (str [ i ] == ‘(’)
            {
                top = top + 1;
                stack[ top ] = ‘ ( ’;
            }
            if(str[ i ] == ‘)’ )
            {
                if(top == -1 )
                {
                    top = top -1 ;
                    break ;
                 }
                else
                {
                     top = top -1 ;
                }
            }
        }
        if(top == -1)
            cout << “String is balanced!” << endl;
        else
            cout << “String is unbalanced!” << endl ;
    }

    int main ( ) 
    {
        //balanced parenthesis string.
        char str[  ] = { ‘(‘ , ‘a’ , ‘+’, ‘ ( ’, ‘b ’ , ‘-’ , ‘ c’ ,‘)’ , ‘ ) ’} ;

        // unbalanced string . 
        char str1 [ ] = { ‘(’ , ‘(’ , ‘a’ , ‘ + ’ , ‘ b’ , ‘)’ } ;
        char stack [ 15 ] ;
        top = -1;   
        check (str , 9 , stack );      //Passing balanced string   
        top = -1 ;
        check(str1 , 5 , stack) ;    //Passing unbalanced string
        return 0;

    } 

Output

String is balanced!  
String is unbalanced!