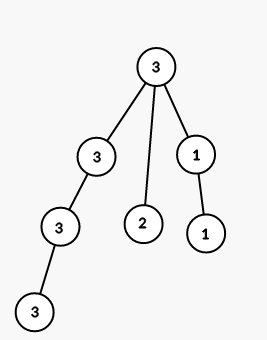
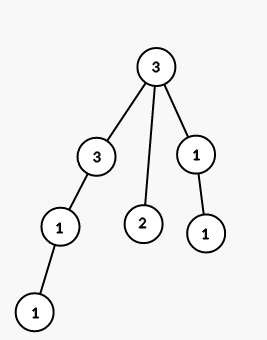
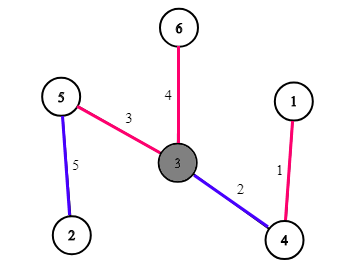
Đề bài: Bạn được cho một đồ thị vô hướng với n đỉnh. Không có chu kỳ cạnh đơn giản với độ dài chẵn trong đó. Hay nói cách khác, không có chu kỳ nào của độ dài chẵn đi qua mỗi cạnh nhiều nhất 1 lần. Chúng ta hãy liệt kê từ 1 đến n.
Bạn phải trả lời q truy vấn. Mỗi truy vấn được mô tả bởi 1 đoạn của đỉnh [l,r] và bạn phải đếm số đoạn con [x;y] của nó (l<=x<=y<=r), thỏa mãn nếu chúng ta xóa tất cả các đỉnh ngoại trừ đoạn [x;y] (bao gồm cả x và y) và cạnh giữa chúng, thì ta được kết quả là đồ thị hai phía.
Đầu vào:
+ Dòng đầu tiên chứa hai số nguyên n và m (1<=n<=3.10^5,1<=m<=3.10^5) - là số đỉnh và số cạnh của đồ thị.
+ m dòng tiếp theo mô tả các cạnh của đồ thị. Dòng thứ i chứa hai số nguyên a(i) và b(i) (1<=a(i),b(i)<=n,a(i)#b(i)), kí hiệu một cạnh giữa hai đỉnh a(i) và b(i). Đảm bảo rằng đồ thị này không chứa khuyên.
+ Dòng tiếp theo số nguyên q (1<=q<=3.10^5)- số truy vấn.
+ q dòng tiếp theo chứa các truy vấn. Dòng thứ i chứa hai số nguyên l(i) và r(i) (1<=l(i)<=r(i)<=n) - tham số truy vấn.
Đầu ra:
In ra q số, mỗi số một dòng. Dòng thứ i là số đoạn con [x;y], thỏa mãn rằng chỉ chứa các đỉnh từ đoạn [x;y] và các cạnh giữa chúng là lưỡng phân.
Ví dụ:
Đầu vào:
6 6
1 2
2 3
3 1
4 5
5 6
6 4
3
1 3
4 6
1 6
Đầu ra:
5
5
14
/***/
Đầu vào:
8 9
1 2
2 3
3 1
4 5
5 6
6 7
7 8
8 4
7 2
3
1 8
1 4
3 8
Đầu ra:
27
8
19.
Chú ý:
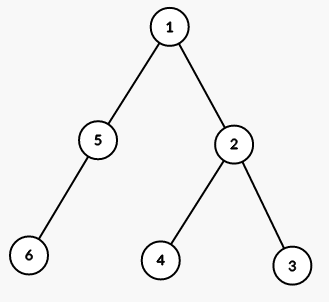
Ví dụ đầu được biểu diễn như sau:
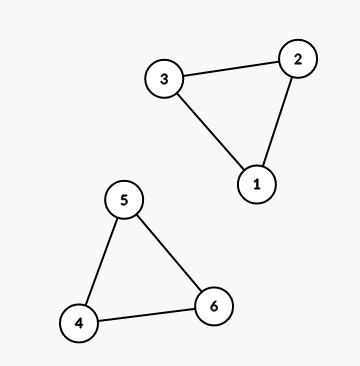
Với truy vấn đầu tiên, tất cả các đoạn con của [1;3], ngoại trừ chính nó, là thích hợp.
Với truy vấn thứ hai, tất cả các đoạn con của [4;6], ngoại trừ chính nó, là thích hợp.
Với truy vấn thứ ba, tất cả các đoạn con của [1;6] là thích hợp, ngoại trừ [1;3],[1;4],[1;5],[1;6],[2;6],[3;6],[4;6].
Ví dụ thứ hai được biểu diễn như hình dưới đây:
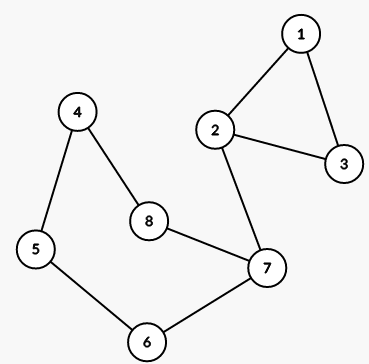
Hướng dẫn: Nếu hai chu kỳ có độ dài lẻ giao nhau, thì chúng có thể bỏ qua để mà đạt được một chu trình có độ dài chẵn của một cạnh đơn giản.
Điều này dẫn tới đồ thị được cho là môt đỉnh cactus (cây xương rồng), với chu trình có độ dài lẻ, vì vậy đoạn đỉnh là tốt - nếu nó không có khuyên, nghĩa là đỉnh với số nhỏ nhất từ chu trình này được hiển thị trên đoạn này và đỉnh với số lớn nhất từ chu trình này hiển thị trên đoạn này. Vì vậy chúng ta có thể chọn tất cả các chu trình, và bây giờ chúng ta làm việc với đoạn.
Chúng ta hãy tìm mỗi đỉnh với biên phải nhỏ nhất trên đoạn, thỏa mãn khoảng [i...mx(i)] là một đồ thị lưỡng phân.
Để trả lời các truy vấn, chúng ta cần phải tổng hợp mx(i)-i+1 cho chúng mà có mx(i)>=r và tổng của r-i+1 cho những cái mà có mx(i)>=r.
Vì vậy, chúng tôi kí hiệu rằng mx(i) tăng và chúng tôi suy ra cần phải tìm thời điểm đầu tiên mà mx(i) trở nên >=r (chúng ta có thể làm việc này với tìm kiếm nhị phân)
Và sau đó tính hai tổng trước - tổng của các (mx(i)-i+1) và tổng của các i.
Lời giải:
#include<bits/stdc++.h> using namespace std; const int N=3e5+7; vector<int>G[N]; int vis[N]={0},p[N]; long long sum[N]={0}; stack<int>s; void dfs(int u,int fa){ s.push(u); vis[u]=1; for(int i=0;i<(int)G[u].size();i++){ int v=G[u][i]; if(v==fa) continue; if(!vis[v]) dfs(v,u); else if(vis[v]==1){ int maxx=u,minn=u; while(!s.empty()){ int t=s.top();s.pop(); maxx=max(t,maxx);minn=min(t,minn); if(t==v) break; } p[minn]=maxx; } } if(!s.empty()&&s.top()==u) s.pop(); vis[u]=2; } int main(){ ios::sync_with_stdio(false);cin.tie(0); int n,m;cin>>n>>m; for(int i=0;i<m;i++){ int x,y;cin>>x>>y; G[x].push_back(y); G[y].push_back(x); } for(int i=1;i<=n+1;i++) p[i]=n+1; for(int i=1;i<=n;i++) if(!vis[i]) dfs(i,-1); for(int i=n;i>=1;i--){ p[i]=min(p[i],p[i+1]); sum[i]=sum[i+1]+p[i]-i; } int q;cin>>q; while(q--){ int l,r;cin>>l>>r; int L=l,R=r+1; while(L<R){ int m=(L+R)/2; if(p[m]>r) R=m; else L=m+1; } cout<<sum[l]-sum[L]+1ll*(r-L+1)*(r-L+2)/2<<endl; } return 0; }