Bài B - Codeforces Round #543 (.Div 2)

Bài B:
Đề bài: Bạn được cho một cái cây có rễ với n đỉnh. Các đỉnh được đánh số từ 1 đến n, rễ cây được đánh số 1.
 Mỗi đỉnh có một màu, chúng ta ký hiệu màu của đỉnh v là c(v). Ban đầu c(v)=0.
  Bạn phải tô màu cho cây thành các màu nhất định sử dụng ít bước nhất có thể. Mỗi bước bạn có thể chọn một đỉnh v và một màu x, và sau đó tô màu tất cả các đỉnh của cây con đỉnh v (bao gồm cả đỉnh v) bằng màu x. Hay nói cách khác, với mỗi đỉnh u, thỏa mãn đường đi từ gốc đến u xuyên qua các đỉnh v, ta đặt c(u)=x.
Đảm bảo rằng bạn phải tô màu mỗi đỉnh bằng một màu khác 0.
Đầu vào:
+ Dòng đầu tiên cho số nguyên n (2<=n<=10^4) - số đỉnh của một cây.
+ Dòng thứ hai chứa n-1 số nguyên p(2),p(3),...,p(n)(1<=p(i)<i), ở đây p(i) có nghĩa là có một cạnh giữa đỉnh đỉnh i và p(i).
+ Dòng thứ ba chứa n số nguyên c(1),c(2),...,c(n) (1<=c(i)<=n), ở đây c(i) là màu bạn nên tô cho đỉnh thứ i.
Đảm bảo rằng đồ thị đã cho là một cây.
Đầu ra:
In một số nguyên- số bước tối thiểu bạn phải thực hiện tô màu bằng các màu nhất định.
Ví dụ:
Đầu vào:
6
1 2 2 1 5
2 1 1 1 1 1
Đầu ra:
3
/********/
Đầu vào:
7
1 1 2 3 1 4
3 3 1 1 1 1 2 3
Đầu ra:
5
/********/
Chú ý:
Cây từ ví dụ đầu tiên được biểu diễn dưới hình dưới đây (các số là chỉ số của các đỉnh)

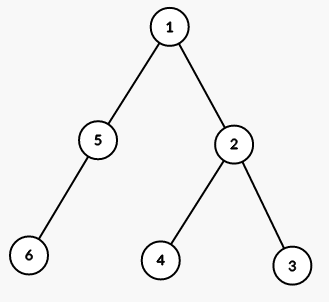
Ở bước đầu tiên ta tô tất cả các đỉnh của cây con của đỉnh 1 bằng màu 2.

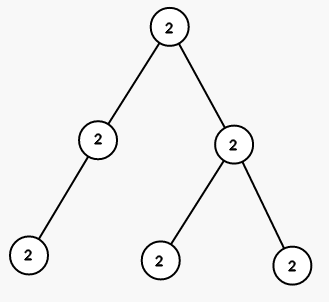
Bước 2 ta tô màu tất cả các đỉnh của cây con đỉnh 5 bằng màu 1

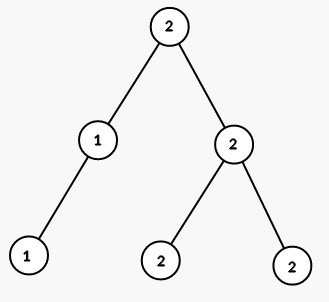
Ở bước thứ 3, ta tô màu tất cả các đỉnh cây con đỉnh 2 bằng màu 1

/***/
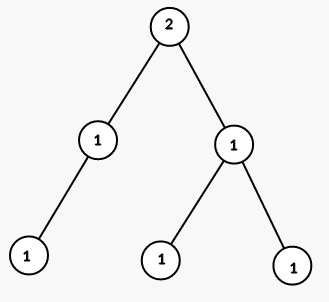
Cây từ ví dụ 2 được biểu diễn như sau:

Ở bước đầu tiên chúng ta tô tất cả các đỉnh của cây con đỉnh 1 bằng màu 3

Ở bước thứ 2 ta tô tất cả các đỉnh của cây con đỉnh 3 bằng màu 1

Ở bước thứ 3 ta tô tất cả các đỉnh của cây con đỉnh 6 bằng màu 2

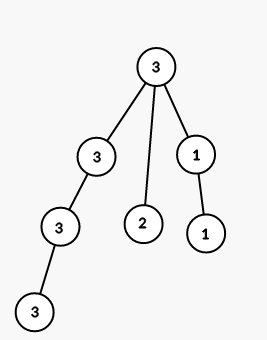
Ở bước thứ 4 chúng ta tô màu tất cả các đỉnh của cây con đỉnh 4 bằng màu 1

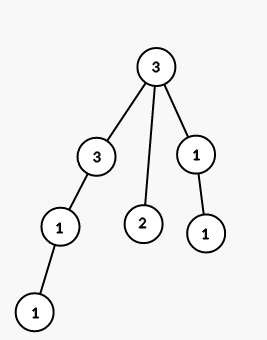
Ở bước thứ 5 ta tô tất cả các đỉnh của cây con đỉnh 7 bằng màu 3

Hướng dẫn: Ta xét quá trình from the end, chúng ta sẽ xóa một cây con bất kì từ cây, màu tổ tiên đỉnh cao nhất của cây con đó phải khác với màu của đỉnh cao nhất và màu của tất cả các đỉnh của cây con phải giống nhau. Vì vậy, chúng ta thể có thể chứng minh được rằng đáp án sẽ là số cạnh mà kết thúc của chúng có số màu khác nhau +1.
Lời giải:

#include<cstdio>
int n,a[10010],f[10100],s,i;
main(){
    scanf("%d",&n);
    for(i=2;i<=n;++i)scanf("%d",f+i);
    for(i=1;i<=n;++i)scanf("%d",a+i),a[i]!=a[f[i]]?++s:0;
    printf("%d",s);
}