Bài G - Codeforces Round #547 (Div.3)

Bài G:

Đề bài: Một vùng đất bao gồm n thành phố và n-1 đường đi. Mỗi đường là đường hai chiều và kết nối hai thành phố phân biệt. Từ bất kì thành phố nào bạn cũng có thể đến bất kì thành phố khác bằng các con đường. Vâng, bạn đã đúng - cấu trúc của miền quê là một cây vô hướng.

 Có một vài công ty tư về đường xá và giao thông trong mãnh đất này. Chính phụ quyết định bán các con đường này cho công ty. Mỗi đường sẽ thuộc về một công ty và một công ty có thể quản lý nhiều đường.

  Chính phủ sợ không công bằng. Họ nghĩ rằng con người trong thành phố này có thể xem họ không công bằng nếu có một công ty mà nó sở hữu hai hoặc nhiều đường vào thành phố. Chính phủ muốn tư nhân hóa rằng số các thành phố như vậy không được quá k và số công ty tham gia vào việc tư nhân hóa này là tối thiểu.

 Chọn số lượng công ty r sao cho có thể chỉ định mỗi con đường cho một công ty theo cách sao cho số lượng thành phố có hai hoặc nhiều con đường của một công ty nhiều nhất là k. Hay nói cách khác, nếu cho một thành phố tất cả các đường thuộc về các công ty khác nhau thì thành phố đó good. Nhiệm vụ của bạn là xác định số r nhỏ nhất để thỏa mãn rằng việc chỉ định các công ty từ 1 đến r thỏa mãn số thành phố không tốt không vượt quá k.

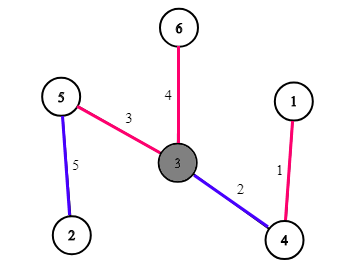
Bức tranh này mô tả ví dụ đầu tiên (n=6,k=2). Câu trả lời là 2 công ty. Các số trên các cạnh kí hiệu chỉ số của cạnh. Các cạnh được tô màu có nghĩa là các công ty: màu đỏ tương ứng với công ty thứ nhất, màu xanh tương ứng với công ty thứ 2. Đỉnh màu xám (số 3) là không tốt. Số đỉnh như vậy (chỉ có 1) không vượt quá k=2. Nó không thể có tối đa k=2 thành phố không tốt trong trường hợp 1 công ty.

Đầu vào: 

+ Dòng đầu tiên chứa hai số nguyên n và k (2<=n<=200000,0<=k<=n-1)- số các thành phố và số thành phố tối đa mà có thể có hai hoặc nhiều đường hơn thuộc về công ty nó.

+ n-1 dòng tiếp theo chứa các đường, mỗi đường một dòng.

Đầu ra: 

+ Dòng đầu tiên chứa số r cần tìm (1<=r<=n-1).

+ Dòng thứ hai in n-1 số c(1),c(2),...,c(n-1)(1<=c(i)<=r), trong đó c(i) là công ty sở hữu đường thứ i. Nếu có nhiều đáp án, in ra đáp án bất kì.

Ví dụ:

Đầu vào:

6 2

1 4

4 3

3 5

3 6

5 2

Đầu ra: 

2

1 2 1 1 2.

Hướng dẫn: Chính thức là, vấn đề ở đây là tô màu các cạnh của cây với số màu tối thiểu theo một cách nào đó sao cho số đỉnh không đúng không vượt quá k. Một đỉnh là không đúng nếu có út nhất hai cạnh trực thuộc cùng màu.

 Dễ dàng chỉ ra rằng D màu luôn luôn đủ để tô cây theo một cách nào đó thỏa mãn tất cả các đỉnh đều đúng, ở đây D là giá trị lớn nhất trong các bậc của đỉnh. Thật vậy, điều này luôn đúng với mọi đồ thị hai phía.

 Trong bài toán này, bạn có thể có tới k đỉnh không đúng, vì vậy chỉ cần chọn d nhỏ nhất sao cho số đỉnh có bậc lớn hơn hoặc bằng d nhiều nhất là k. Trong giải pháp khác là bạn có thể sử dụng tìm kiếm nhị phân để tìm số d như vậy, nhưng nó khó thực hiện hơn và giải pháp này trở nên chậm hơn do nhân tố log.

 Sau khi nó tô các cạnh cạnh với d màu, mỗi lần chọn một màu tiếp theo (bỏ qua màu nếu nó bằng với số màu của cạnh đang duyệt tới).

Lời giải:

#include<bits/stdc++.h>
using namespace std;
int n, k, r;
vector<vector<pair<int,int>>> g;
int D;
vector<int> col;

void dfs(int u, int p, int f) {
    int color = 0;
    for (auto e: g[u])
        if (p != e.first) {
            if (color == f) {
                color = (color + 1) % D;
                f = -1;
            }
            col[e.second] = color;
            dfs(e.first, u, color);
            color = (color + 1) % D;
        }         
}

int main() {
    cin >> n >> k;
    g.resize(n);
    vector<int> d(n);
    for (int i = 0; i + 1 < n; i++) {
        int x, y;
        cin >> x >> y;
        x--, y--;
        g[x].push_back({y, i});
        g[y].push_back({x, i});
        d[x]++, d[y]++;
    }
    map<int,int> cnt;
    for (int dd: d)
        cnt[dd]++;
    
    int kk = n;
    D = 0;
    for (auto p: cnt)
        if (kk > k)
            D = p.first,
            kk -= p.second;
        else
            break;
    col = vector<int>(n - 1);
    dfs(0, -1, -1);    
    cout << D << endl;
    for (int i = 0; i + 1 < n; i++)
        cout << col[i] + 1 << " ";
}