Bài A - Lyft Level 5 Challenge 2018 - Elimination Round

Bài A:
Đề bài: Alice và Bob đang chơi cờ vua trên một bàn cờ lớn với kích thước nxn. Alice chỉ còn lại 1 con cờ - con hậu, đang ở vị trí (a(x),a(y)), trong khi đó Bob chỉ còn một con vua đang ở vị trí (b(x),b(y)). Alice nghĩ rằng con hậu của cô ấy sẽ thống trị cả bàn cờ, và chiến thắng sẽ thuộc về cô ấy.
Nhưng Bob đã thực hiện một kế hoạch lệch lạc (devious plan) để giành lấy (seize) cho mình - Anh ta cần phải hành quân (march) con vua của mình đến điểm (C(x),C(y)) để tuyên bố rằng chiến thắng thuộc về anh ấy. Bởi vì Alice bị phân tâm (distracted) bởi cảm giác vượt trội của mình (her sense of superiority),  nên cô ấy đã không còn miếng nào để di chuyển xung quanh nữa, and chỉ có Bob là người thực hiện bất kỳ bước ngoặt nào.
 Bob sẽ giành chiến thắng nếu anh ấy có thể di chuyển con vua của mình từ (b(x),b(y)) đến (c(x),c(y)) mà không nhận được trong kiểm tra. Hãy nhớ rằng, con vua có thể di chuyển bất kì ô nào trong 8 ô vuông liền kề. Một con vua là đang kiểm tra nếu nó cùng rank ( nghĩa là hàng) và file (cột) hay đường chéo (diagonal) mà con hậu chiếu.
Kiểm tra liệu rằng Bob có thể win hay không.
Đầu vào:
+ Dòng đầu tiên chứa số nguyên n (3<=n<=1000) - kích thước của bàn cờ.
+ Dòng thứ hai chứa hai số nguyên a(x) và a(y) (1<=a(x),a(y)<=n) - là tọa độ con hậu của Alice.
+ Dòng thứ ba chứa hai số nguyên b(x) và b(y) (1<=b(x),b(y)<=n) - là tọa độ con vua của Bob.
+ Dòng thứ tư chứa hai số nguyên c(x) và c(y) (1<=c(x),c(y)<=n) - là tọa độ của vị trí mà Bob cần muốn tới.
Đảm bảo rằng con vua của Bob không bị chiếu và vị trí cần tới cũng không bị chiếu.
Hơn nữa, con vua không ở cùng vị trí với con hậu nghĩa là (a(x)#b(x) hay a(y)#b(y)) và vị trí muốn tới cũng không trùng (coincide) với vị trí của con hậu (nghĩa là c(x)#a(x) hoặc c(y)#a(y)).
Đầu ra:
In ra YES nếu Bob có thể đi từ (b(x),b(y)) đến (c(x),c(y)) mà không bị chiếu, ngược lại in ra NO
Ví dụ:
Đầu vào:
8
4 4
1 3
3 1
Đầu ra:
YES
/**/
Đầu vào:
8
4 4
2 3
1 6
Đầu ra:
NO.
/***/
Đầu vào:
8
3 5
1 2
6 1
Đầu ra:
NO
Chú ý:
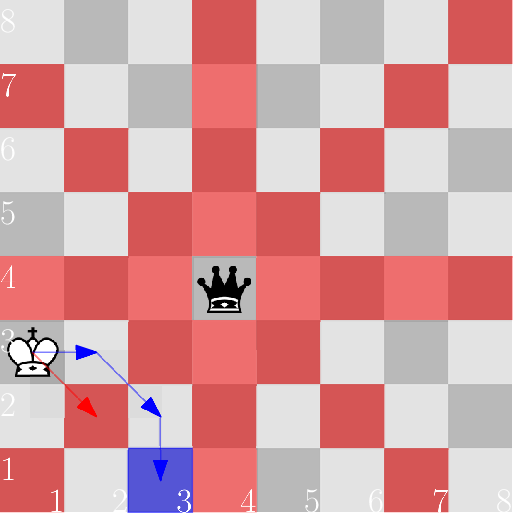
Trong các hình dưới đây, các ô vuông được điều khiển bởi con hậu đen được đánh dấu đỏ, và ô mục tiêu được đánh dấu xanh.
Ở trong trường hợp đầu tiên, con vua di chuyển, ví dụ (for instance), bằng ô vuông (2,3) và (3,2). Chú ý rằng đi đường trực tiếp qua ô (2,2) bị chiếu.

Ở trường hợp 2,

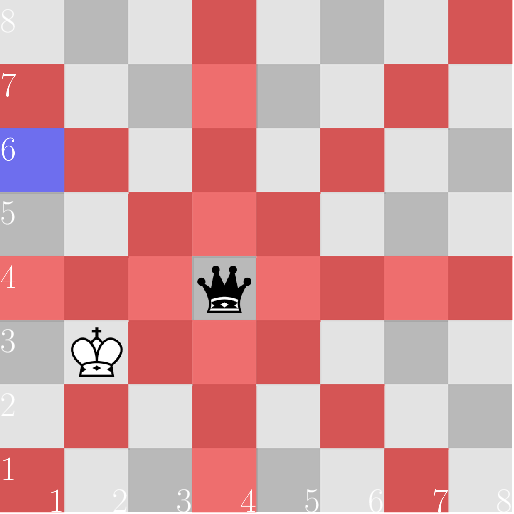
Ở trường hợp 3,

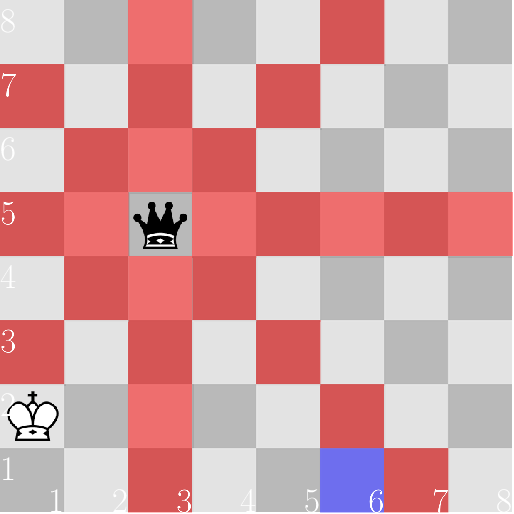
Hướng dẫn:
Tưởng tượng rằng 1 mặt phẳng 2 chiều với vị trí nguyên thủy của con hậu. Chúng ta chú ý rằng con hậu sẽ chia bảng thành 4 thành phần liên kết với mỗi góc phần tư là một trong số họ. Câu trả lời là YES khi và chỉ khi vị trí của con vua và vị trí đích cùng 1 phần tư.
Điều kiện này có thể được kiểm tra bằng O(1) thông qua một số lệnh if đơn giản.
 Trong trường hợp bạn thích chạy trâu hơn phân tích trường hợp, bạn có thể xây dựng biểu đồ lưới và tìm các thành phần được kết nối hoặc sử dụng dfs để tìm đường dẫn. Cái này chạy với O(n^2).
Lời giải:

#include<bits/stdc++.h>
using namespace std;
int n,ax,ay,bx,by,cx,cy;
int main(){
 cin>>n>>ax>>ay>>bx>>by>>cx>>cy;
 bx-=ax,by-=ay,cx-=ax,cy-=ay;
 cout<<(bx*cx>0&&by*cy>0?"YES":"NO");
}