Bài C - Google Bye 2018

Bài C:
Đề bài: Cho n người ngồi theo 1 vòng tròn, được đánh số từ 1 đến n. Có nghĩa là, với mọi i chạy từ 1 đến n-1, thì người có chỉ số i và i+1 ngồi kề nhau. Người thứ n và người thứ 1 cũng ngồi kề nhau.
Người với chỉ số là 1 ban đầu có 1 trái bóng. Anh ta lấy một số nguyên k (k<=n), và chuyền trái banh này đến người hàng xóm thứ k của anh ta theo chiều tăng dần của các chỉ số, người đó chuyền bóng cho người hàng xóm thứ k của mình theo cùng hướng, và cứ thế cho đến khi người với chỉ số 1 nhận được bóng. Khi anh ta nhận được bóng, mọi người sẽ không chuyền bóng nữa.
Ví dụ, nếu n=6 và k=4, thì quả bóng sẽ được chuyển theo thứ tự [1,5,3,1].
 Xét tập tất cả các người mà chạm vào quả bóng. Độ vui của game là tổng các chỉ số của người mà chạm vào quả bóng. Ở trường hợp trên, độ vui của game là 1+5+3=9.
Tìm và báo cáo tập các giá trị vui có thể cho tất cả các lựa chọn số nguyên dương k. Có thể chỉ ra ràng buộc của vấn đề quả bóng cuối cùng luôn ở trong tạy người thứ 1 sau nhiều bước chuyền bóng chính xác và không có quá 105 giá trị vui có thể của n.
Đầu vào:
+ Dòng đầu tiên chứa số nguyên n (2<=n<=10^9) - số lượng người chơi bóng.
Đầu ra:
+ Giả sử ta có một tập các giá trị vui là f(1),f(2),....,f(m)
+ In ra một 1 dòng duy nhất chứa m số từ f(1) đến f(m) theo thứ tự tăng dần.
Ví dụ:
Đầu vào:
6
Đầu ra:
1 5 9 21
Đầu vào:
16
Đầu ra:
1 10 28 64 136
Chú thích:
Ở ví dụ đầu tiên, chúng ta đã có sẵn với k=4, chúng ta được giá trị vui vẻ là 9, cũng như với k=2. Với k=6, ta được giá trị vui vẻ là 1. Ứng với k=3, ta được giá trị vui vẻ là 5, và ứng với k=1 hoặc 5, giá trị vui vẻ là 21.

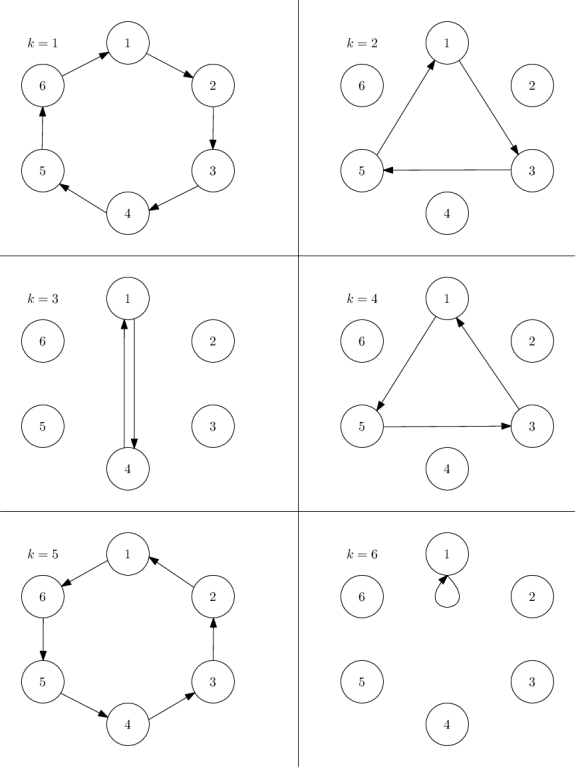
Ở ví dụ 2, các giá trị 1,10,28,64 và 136 đạt được là với k=16,8,4,10 và 11 lần lượt.
Hướng dẫn:
 Trừ 1 từ tất cả các giá trị cho tiện. Điều chỉnh giá trị k. Chúng ta được các giá trị a.k mod n với a từ 0 cho đến đạt 0 lại. Giá trị này có thể được viết a.k-b.n. Theo định lý Bezout, phương trình a.k-b.n=c có nghiệm cho a và b khi và chỉ khi c chia hết cho gcd(k,n).
Hơn thế nữa, tất cả các giá trị của c sẽ được duyệt qua trước khi nó quay về 0. Ở đây, bởi vì phần từ k/gcd(k,n) sinh ra nhóm $\mathbb{Z}_{n/gcd(k,n)}$.
Chúng ta có thể xét các giá trị k là ước của n. Chúng ta có thể tìm tất cả chúng bằng độ phức tạp $O(\sqrt{n})$. Với mỗi trong số chúng, chúng ta có thể tìm một giải pháp dạng đóng bằng cách tổng hợp chuỗi số học.
Lời giải:

#include <bits/stdc++.h>
using namespace std;

int main()
{
 long long n,i,x;
 cin>>n;
 set<long long> a;
 for(i=1;i*i<=n;i++){
  if(n%i) continue;
  x=n/i;
  a.insert((1+n-i+1)*x/2);
  a.insert((1+n-x+1)*i/2);
 }
 for(auto it:a) printf("%lld\n",it);
 return 0;
}